Transformasi Bilinear

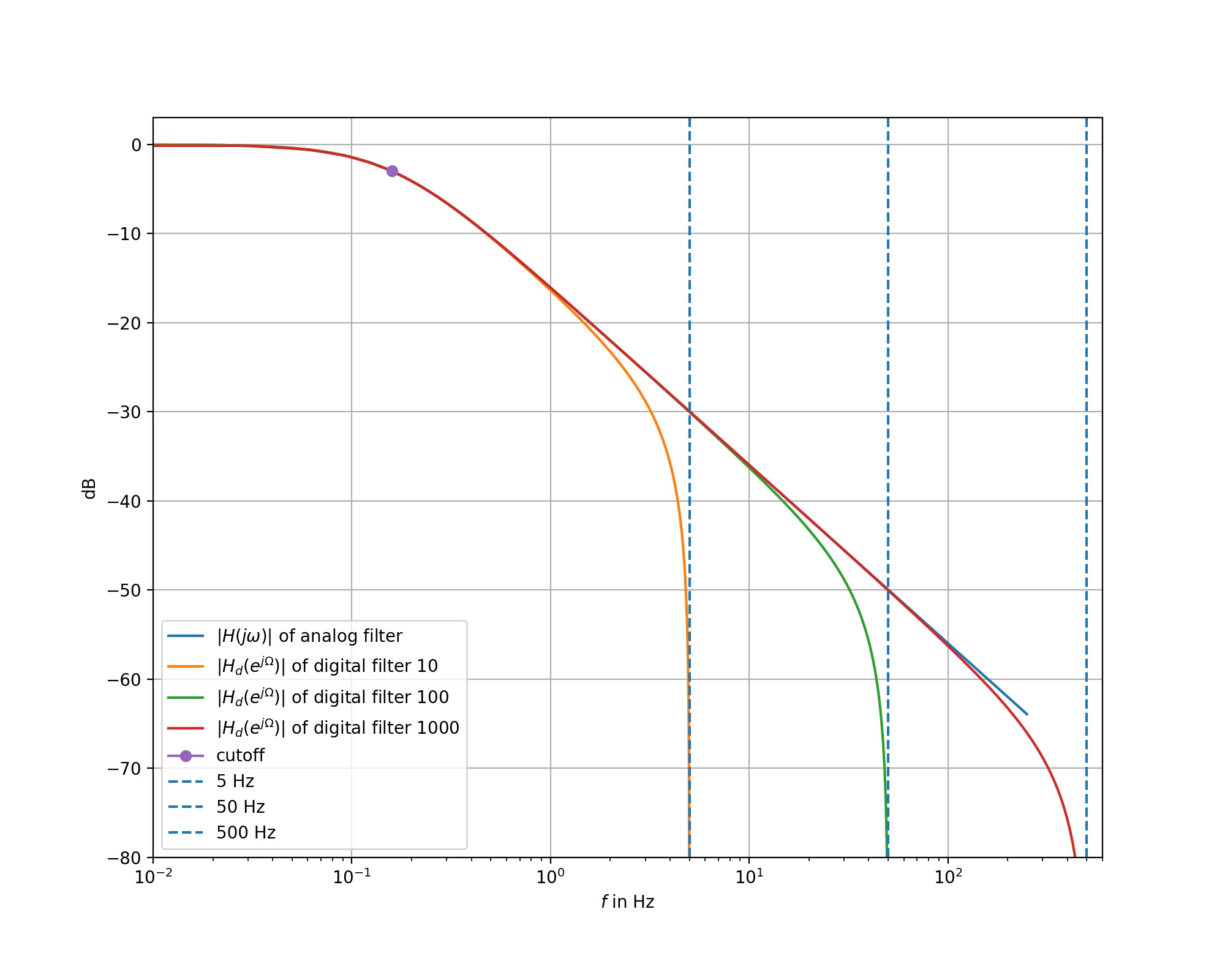
Respon Frekuensi LPF orde 1

Percobaan melihat pengaruh frekuensi sampling terhadap fungsi transfer sistem orde 1 low pass

Fungsi transfer sistem = 1/(s+1)

Time constant = 1, sehingga frekuensi cut off adalah 0.159 Hz

Gambar ilustrasi fungsi transfer untuk filter analog dan filter digital.

Filter digital dicoba dengan beberapa frekuensi sampling: 10 Hz, 100 Hz, 1000 Hz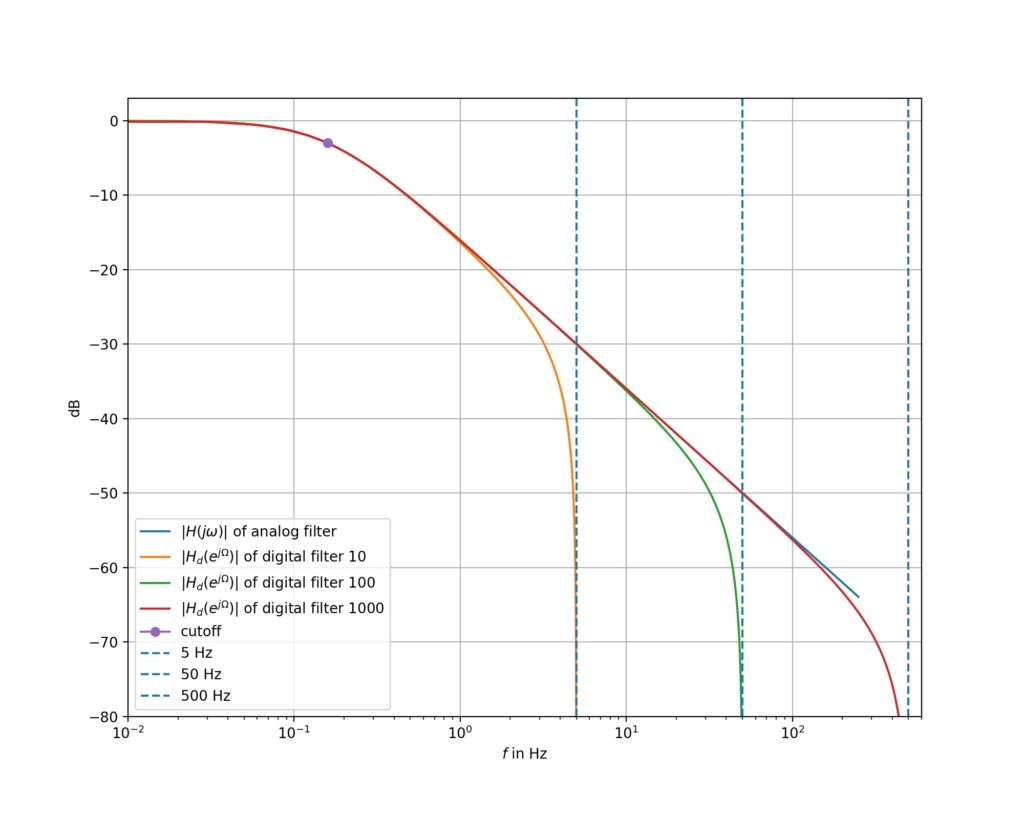

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
%matplotlib inline

B = [0, 1]
A = [1, 1]

fs10= 10
fs100= 100
fs1000= 1000

fs10_z   = signal.bilinear(B,A,fs10)
fs100_z  = signal.bilinear(B,A,fs100)
fs1000_z = signal.bilinear(B,A,fs1000)

fs10_a  =fs10_z[1]
fs10_b  =fs10_z[0]

fs100_a =fs100_z[1]
fs100_b =fs100_z[0]

fs1000_a=fs1000_z[1]
fs1000_b=fs1000_z[0]
# displaying
plt.figure(figsize=(10, 8))
Om, fs10_Hd   = signal.freqz(fs10_b  , fs10_a, worN=1024)
f10 = Om * fs10 / (2 * np.pi)

Om, fs100_Hd  = signal.freqz(fs100_b , fs100_a, worN=2048)
f100 = Om * fs100 / (2 * np.pi)

Om, fs1000_Hd = signal.freqz(fs1000_b, fs1000_a, worN=16384) # 1000 Hz mesti lebih banyak sampelnya
f1000 = Om * fs1000 / (2 * np.pi)

tmp, H = signal.freqs(B, A, worN=f1000 * Om)
f = Om * f1000 / (2 * np.pi)

plt.semilogx(f, 20 * np.log10(np.abs(H)), label=r"$|H(j \omega)|$ of analog filter")
plt.semilogx(f10, 20 * np.log10(np.abs(fs10_Hd)), label=r"$|H_d(e^{j \Omega})|$ of digital filter 10")
plt.semilogx(f100, 20 * np.log10(np.abs(fs100_Hd)), label=r"$|H_d(e^{j \Omega})|$ of digital filter 100")
plt.semilogx(f1000, 20 * np.log10(np.abs(fs1000_Hd)), label=r"$|H_d(e^{j \Omega})|$ of digital filter 1000")
plt.semilogx(0.159, 20 * np.log10(0.707), marker='o',label="cutoff")
plt.axvline(x = 10/2,   linestyle="--", label = '5 Hz')
plt.axvline(x = 100/2,  linestyle="--", label = '50 Hz')
plt.axvline(x = 1000/2, linestyle="--", label = '500 Hz')
plt.xlabel(r"$f$ in Hz")
plt.ylabel(r"dB")
plt.axis([0.01, 600, -80, 3])
plt.legend()
plt.grid()
plt.savefig("first-order.jpg",dpi=200)
# https://www.geeksforgeeks.org/plot-a-vertical-line-in-matplotlib/

Analisis

• frekuensi warping kelihatan di frekuensi yang makin dekat dengan 1/2 frekuensi sampling
• frekuensi cut off tidak terpengaruh

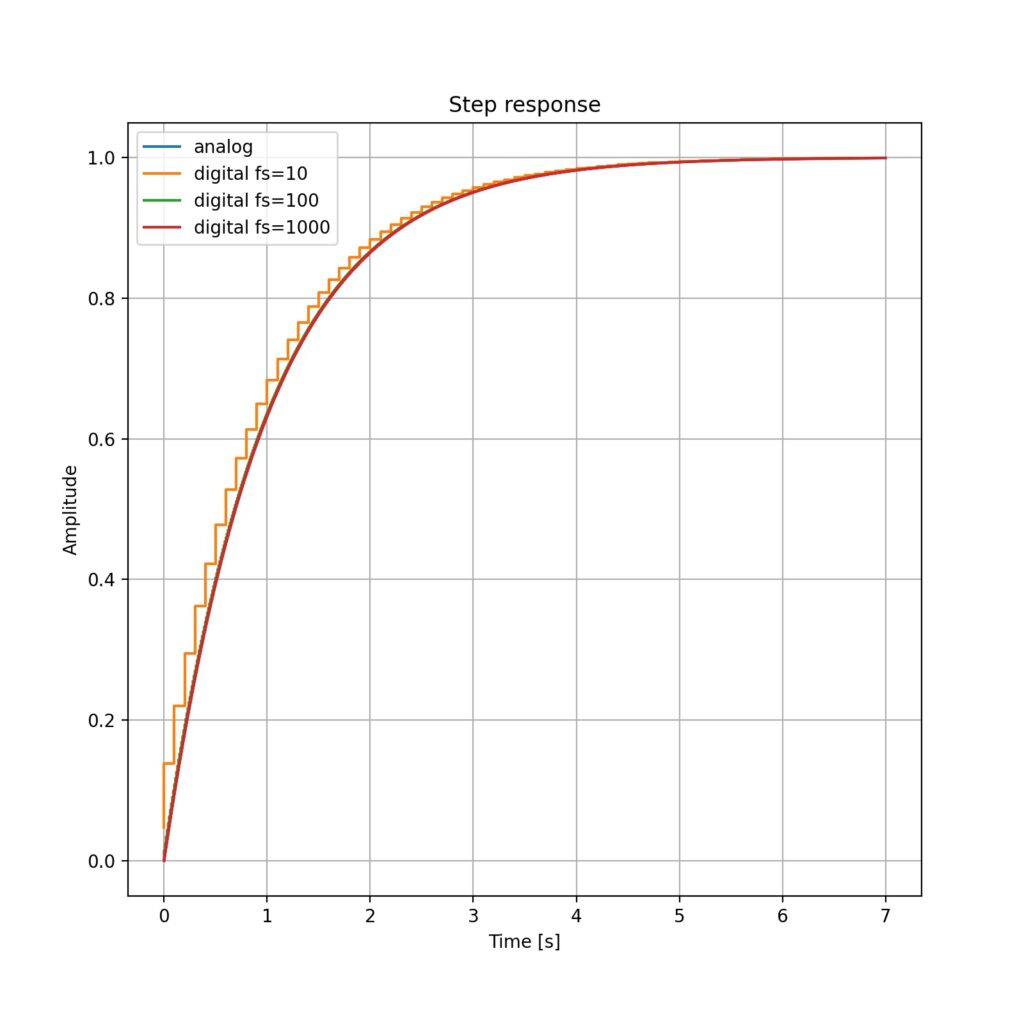
Respon Step Low Pass Filter orde 1

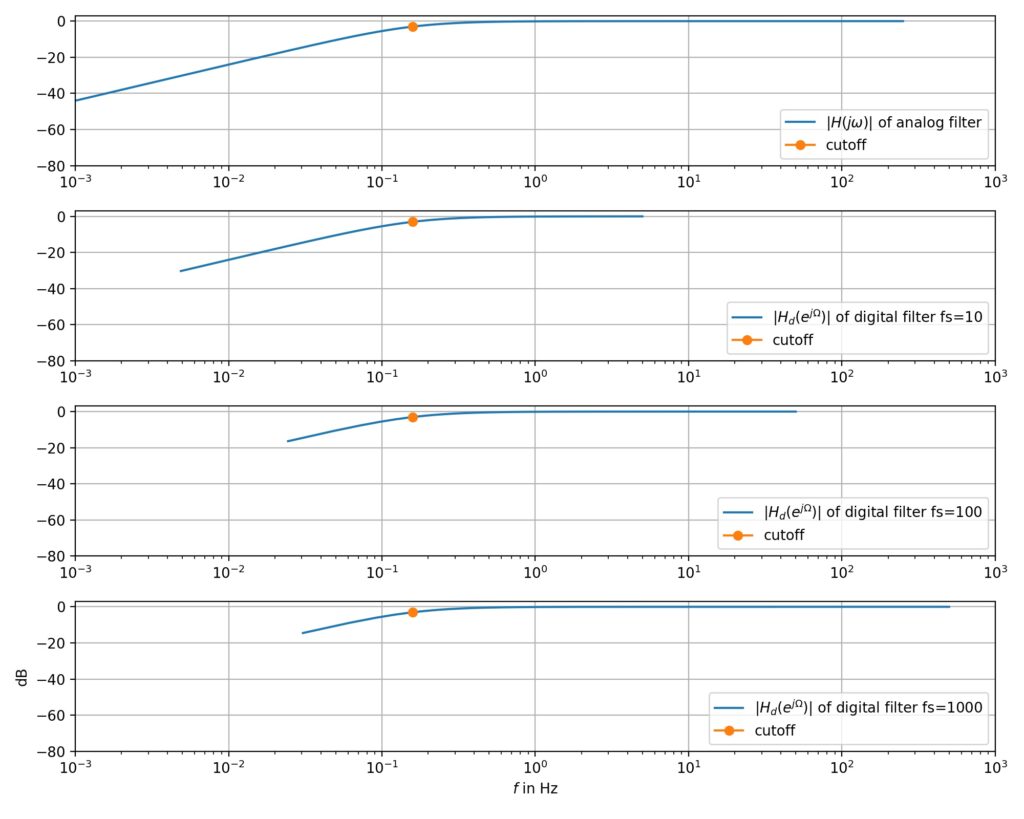
Respon Frekuensi High Pass Filter orde 1

Kesimpulan:

• perubahan frekuensi sampling tidak mengubah banyak respon frekuensi filter

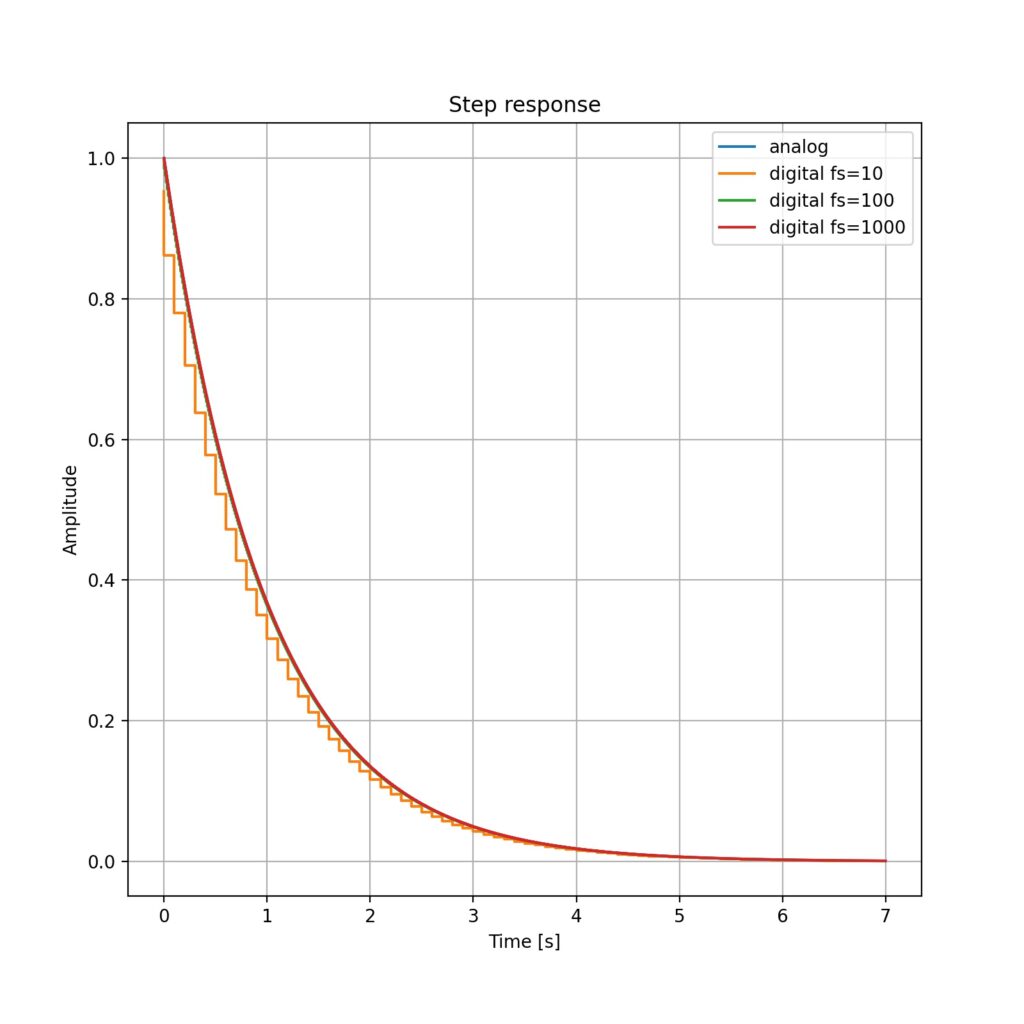
Respon Step High Pass Filter orde 1

Kesimpulan:

• perubahan frekuensi sampling tidak banyak mengubah bentuk sinyal, kecual pada fs = 10 Hz