Daftar Isi
Perancangan Filter
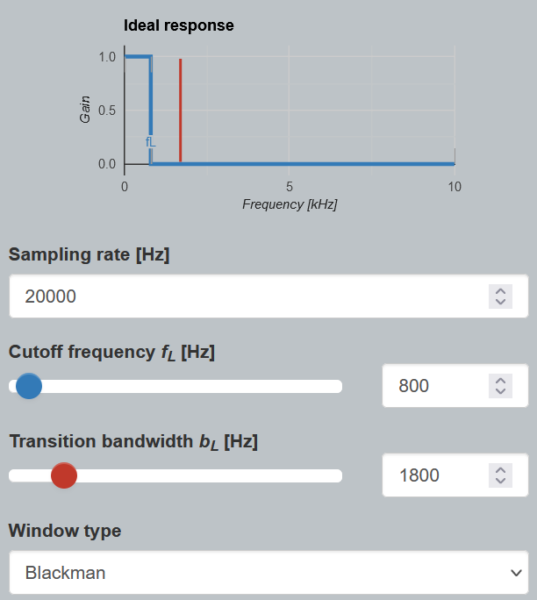
Perancangan filter menggunakan tools dari https://fiiir.com/
Parameter yang digunakan:
- Sampling rate: 20000 Hz
- Cut off frequency 800 Hz
- Transition bandwidth 1800 Hz
- Window type : Blackman
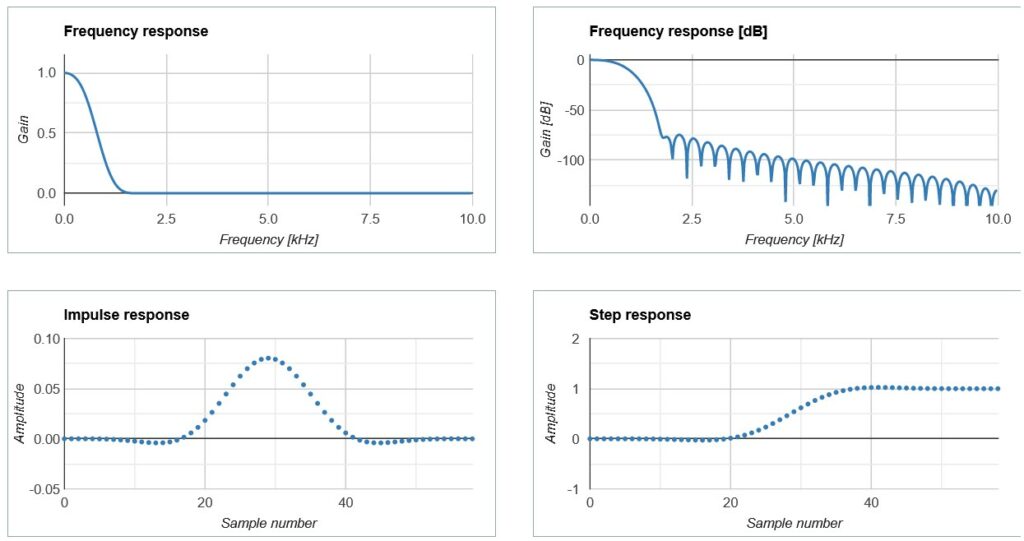
Berikut ini karakteristik filter yang dapat dilihat di laman yang sama
Kode dalam bahasa Python untuk menghitung parameter filter dan konvolusinya juga dihasilkan dari laman yang sama, sebagai berikut:
from __future__ import print_function |
Parameter filter yang dihasilkan adalah sebagai berikut (sebagai Python array)
[-4.29317419e-20 -4.18549678e-21 -1.79819385e-05 -8.38178513e-05 -2.28616892e-04 -4.79528638e-04 -8.51847897e-04 -1.33864303e-03 -1.89910369e-03 -2.44776137e-03 -2.84740649e-03 -2.90866942e-03 -2.39870072e-03 -1.06016948e-03 1.35995551e-03 5.07437980e-03 1.02166209e-02 1.68050560e-02 2.47160945e-02 3.36720917e-02 4.32479500e-02 5.28978134e-02 6.20002342e-02 6.99171799e-02 7.60597872e-02 7.99523091e-02 8.12855501e-02 7.99523091e-02 7.60597872e-02 6.99171799e-02 6.20002342e-02 5.28978134e-02 4.32479500e-02 3.36720917e-02 2.47160945e-02 1.68050560e-02 1.02166209e-02 5.07437980e-03 1.35995551e-03 -1.06016948e-03 -2.39870072e-03 -2.90866942e-03 -2.84740649e-03 -2.44776137e-03 -1.89910369e-03 -1.33864303e-03 -8.51847897e-04 -4.79528638e-04 -2.28616892e-04 -8.38178513e-05 -1.79819385e-05 -4.18549678e-21 -4.29317419e-20] |
Simulasi dengan Python di Desktop
Berikut ini kode untuk simulasi filter tersebut di Jupyter Notebook dengan bahasa Python.
from __future__ import print_function |
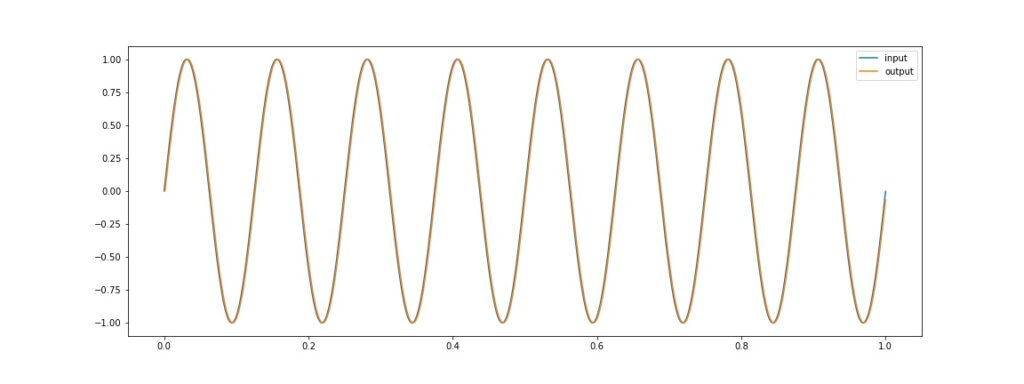
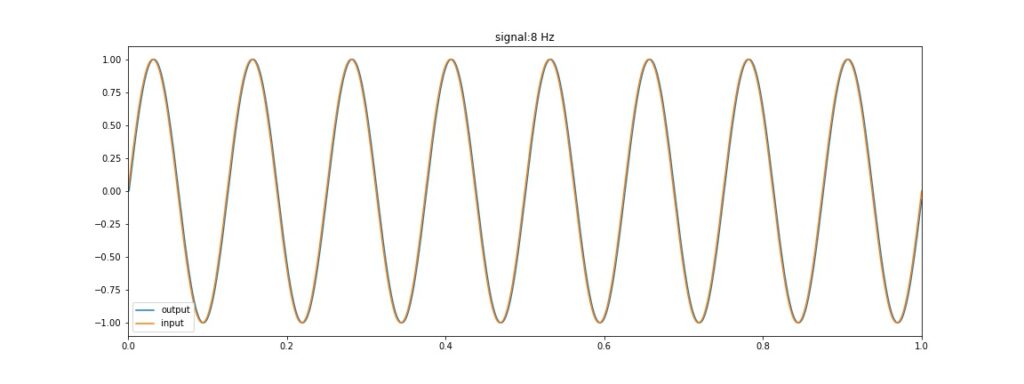
Hasil simulasi untuk frekuensi 8 Hz
 Hasil simulasi untuk frekuensi 80 Hz
Hasil simulasi untuk frekuensi 80 Hz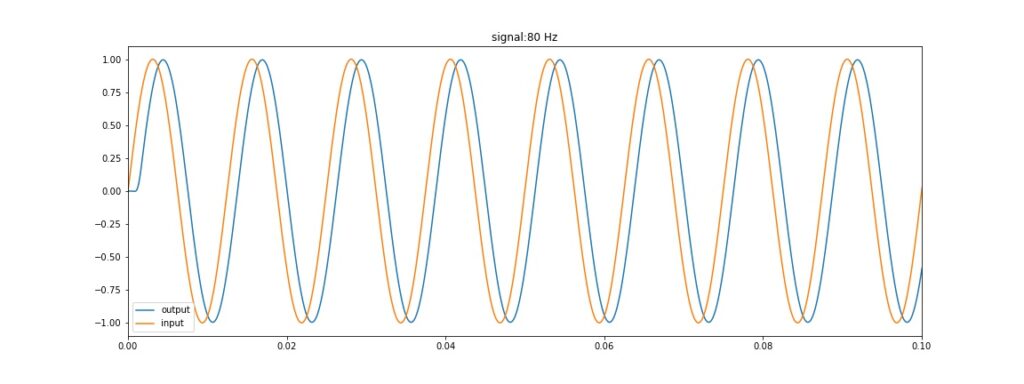 Hasil simulasi untuk frekuensi 800 Hz
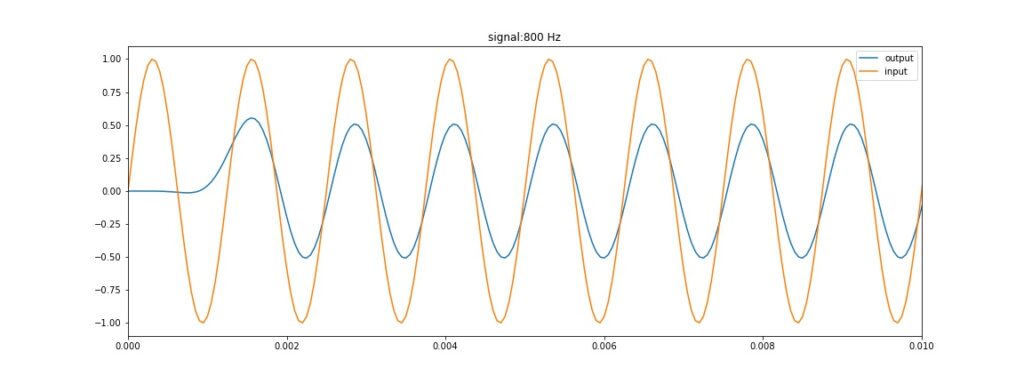
Hasil simulasi untuk frekuensi 800 Hz
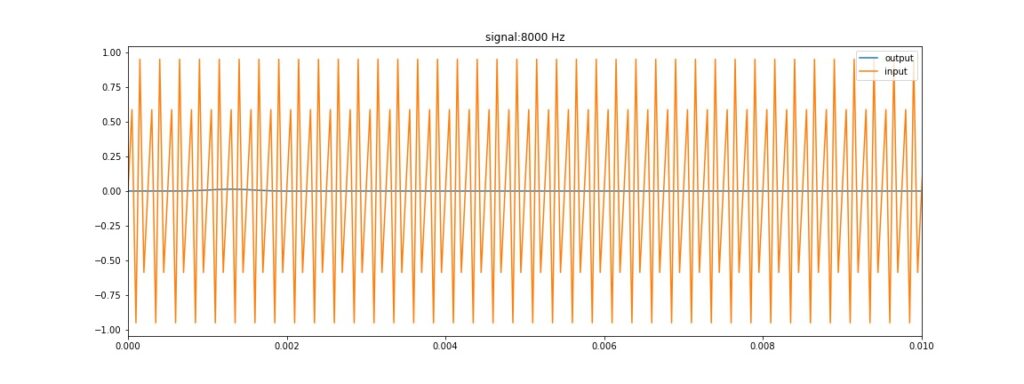
Hasil simulasi untuk frekuensi 8000 Hz
Simulasi dengan C di Desktop
Pada percobaan ini filter disimulasikan di Desktop PC untuk mengecek ketepatan perhitungan dibandingkan dengan versi Python.
Kode untuk simulasi C sebagai berikut:
#include <stdio.h> |
Output kode C tersebut berupa file *.csv
Visualisasi data di file *.csv dilakukan menggunakan Jupyter Notebook dengan kode sebagai berikut:
import pandas as pd |
Tampilan Visualisasi untuk sinyal 8 Hz
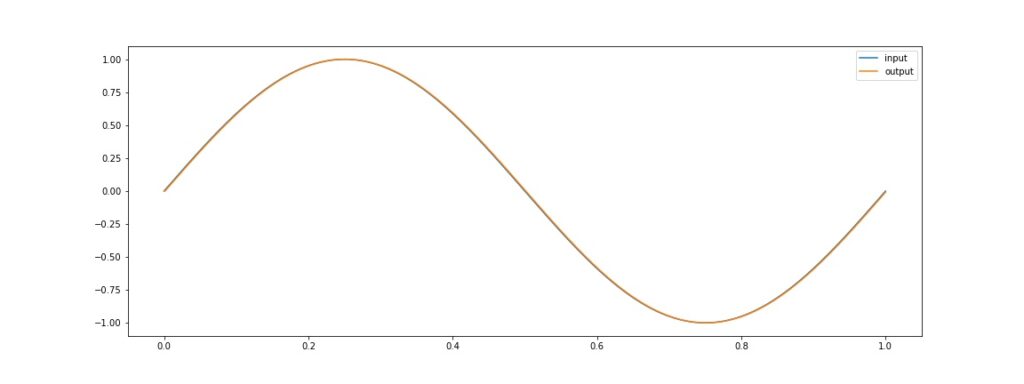 nampak sinyal 8 Hz tidak teredam
nampak sinyal 8 Hz tidak teredam
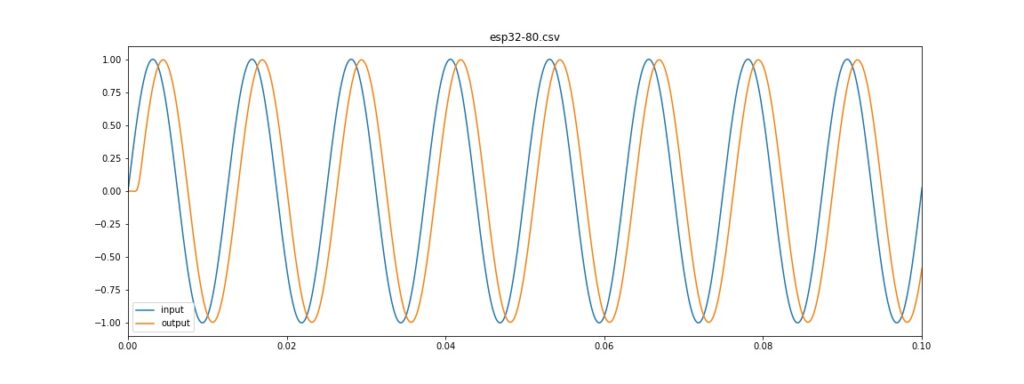
Tampilan Visualisasi untuk sinyal 80 Hz
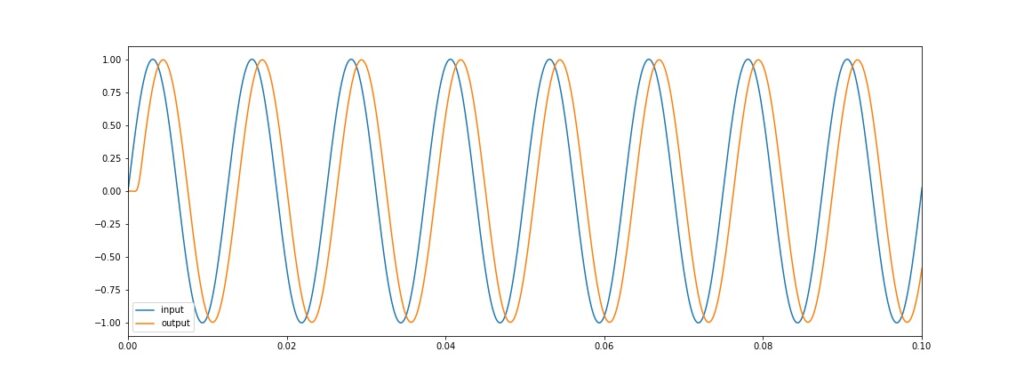 sinyal 80 Hz nampak teredam sedikit sekali dan ada lag
sinyal 80 Hz nampak teredam sedikit sekali dan ada lag
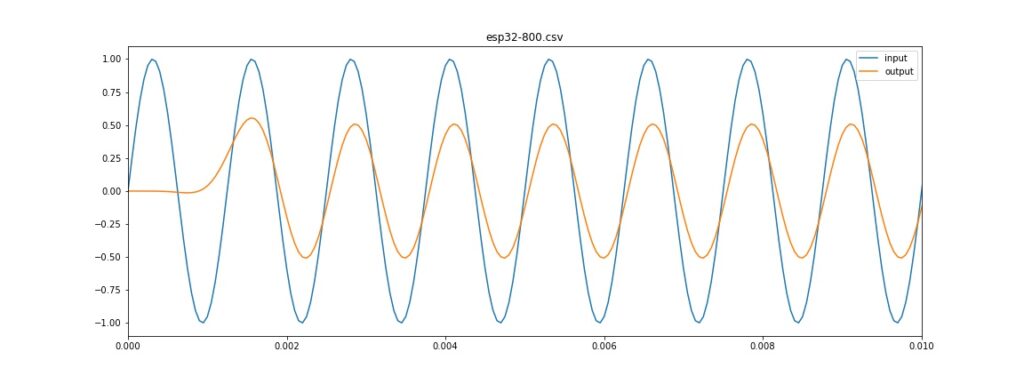
Tampilan Visualisasi untuk sinyal 800 Hz
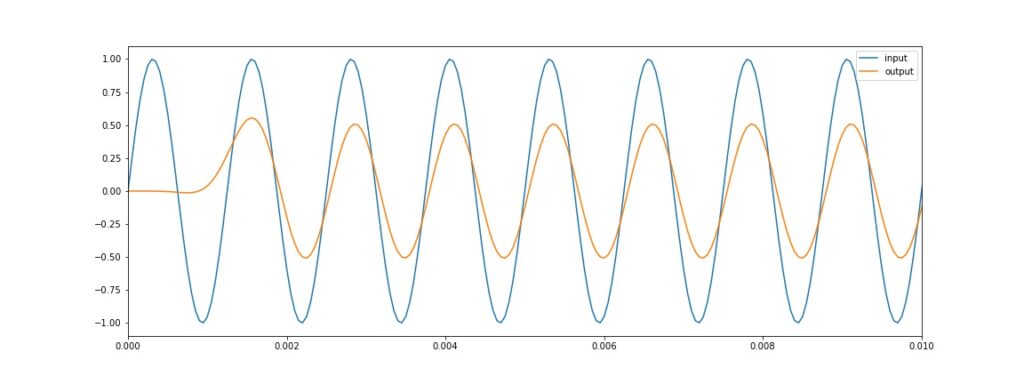 nampak sinyal 800 Hz teredam sekitar 50%
nampak sinyal 800 Hz teredam sekitar 50%
Tampilan Visualisasi untuk sinyal 8000 Hz
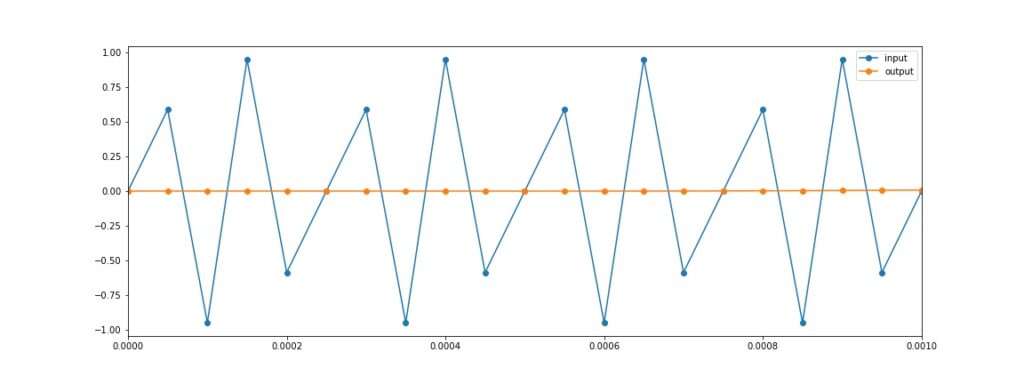 nampak sinyal 8000 Hz teredam hampir semuanya
nampak sinyal 8000 Hz teredam hampir semuanya
Simulasi dengan C di ESP32
pada percobaan ini kode dijalankan di ESP32 namun input adalah simulasi bukan dari generator sinyal. Output direkam ke port serial, bukan ke osiloskop.
Kode ESP32 adalah sebagai berikut
#define ORDE_FILTER 53 |
Output dari ESP32 direkam dengan software RealTerm ke sebuah file *.txt
File *.txt tersebut dirapikan dan disimpan sebagai *.csv
File *.csv ini kemudian divisualisasikan dengan Jupyter Notebook
Kode visualisasi sebagai berikut
# graph simulasi C filter |
Sinyal 80 Hz
Sinyal 800 Hz
Sinyal 8000 Hz
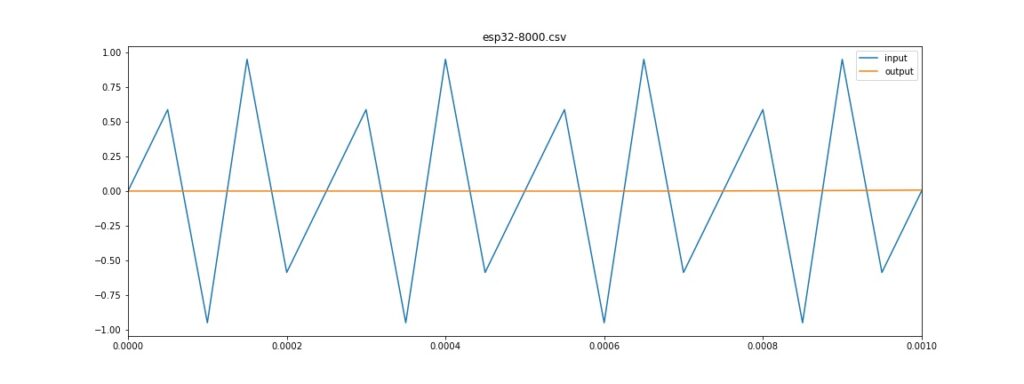 Kesimpulan: output dari software LPF di ESP32 sama dengan output dari software C di Desktop
Kesimpulan: output dari software LPF di ESP32 sama dengan output dari software C di Desktop
Profiling di ESP32
Pada percobaan ini waktu yang diperlukan untuk menghitung filter diukur di ESP32.
Pewaktuan menggunakan fungsi millis(). Fungsi millis() tidak 100% akurat. Untuk lebih tepat perlu interupsi timer, atau dengan osiloskop.
Kode profiling:
|
#define ORDE_FILTER 53
float buffer[100];
void setup() {
int buffer_index = 0;
int durasi;
Serial.begin(115200);
//
long int i;
int j, k;
char filename[100];
// simulasi 1 detik saja
float signal_frequency = 8; // frekuensi input signal
float filter_coefficients[] = { -4.29317419e-20, -4.18549678e-21, -1.79819385e-05, -8.38178513e-05,
-2.28616892e-04, -4.79528638e-04, -8.51847897e-04, -1.33864303e-03,
-1.89910369e-03, -2.44776137e-03, -2.84740649e-03, -2.90866942e-03,
-2.39870072e-03, -1.06016948e-03, 1.35995551e-03, 5.07437980e-03,
1.02166209e-02, 1.68050560e-02, 2.47160945e-02, 3.36720917e-02,
4.32479500e-02, 5.28978134e-02, 6.20002342e-02, 6.99171799e-02,
7.60597872e-02, 7.99523091e-02, 8.12855501e-02, 7.99523091e-02,
7.60597872e-02, 6.99171799e-02, 6.20002342e-02, 5.28978134e-02,
4.32479500e-02, 3.36720917e-02, 2.47160945e-02, 1.68050560e-02,
1.02166209e-02, 5.07437980e-03, 1.35995551e-03, -1.06016948e-03,
-2.39870072e-03, -2.90866942e-03, -2.84740649e-03, -2.44776137e-03,
-1.89910369e-03, -1.33864303e-03, -8.51847897e-04, -4.79528638e-04,
-2.28616892e-04, -8.38178513e-05, -1.79819385e-05, -4.18549678e-21,
-4.29317419e-20 };
int orde_filter = ORDE_FILTER;
float y_history[ORDE_FILTER];
signal_frequency = 800;
// signal_frequency = 80;
// signal_frequency = 8;
printf(“time,y,y_out\n”);
// zeros y_history
for (i = 0; i < orde_filter; i++) {
y_history[i] = 0;
}
int time_start = millis();
for (i = 0; i < 1000000L; i++) {
float t, y;
t = (float)i / (float)20000; // time axis
y = sin(2 * M_PI * signal_frequency * t);
// fprintf(fp,”%f,%f\n”,t,y);
// hitung history signal
for (j = orde_filter – 1; j >= 1; j–) {
int src = j – 1;
int dst = j;
y_history[dst] = y_history[src];
// printf(“%d %d\n”,src,dst);
}
y_history[0] = y;
// hitung konvolusi
float y_out = 0;
for (k = 0; k < orde_filter; k++) {
y_out = y_out + y_history[k] * filter_coefficients[k];
}
// fprintf(fp,”\n”);
// Serial.print(“.”);
buffer[buffer_index] = y_out;
buffer_index++;
if (buffer_index>100){
buffer_index=0;
}
}
int time_end = millis();
durasi = time_end – time_start;
Serial.println(“durasi”);
Serial.println(durasi);
}
void loop() {
// put your main code here, to run repeatedly:
}
|
Hasil profiling: kode memerlukan 16479 ms untuk menjalankan 1000000 kali perhitungan. jadi setiap perhitungan memerlukan 16.479 us
Konversi DAC di ESP32 memerlukan sekitar 20 us (pesimis), jadi jika kode sekuensial maka didapatkan perioda 36.479 us, atau frekuensi = 27413 Hz.
Frekuensi filter yang dirancang adalah 20000 Hz, jadi masih di bawah batas 27413 Hz.
Pengujian Dengan Sinyal Sesungguhnya
Pada percobaan ini kode dijalankan di ESP32 dengan input dari generator sinyal dan output diamati di osiloskop
Berikut ini implementasi rangkaian:

Implementasi software dapat dilihat di https://github.com/waskita/embedded/tree/master/esp32_mcp3008_baker_adc_dac_filter-timer
Sinual input didapat dari generator sinyal GW Instek AFG-2012
Pengukuran output menggunakan osiloskop GW Instek-1152A-U
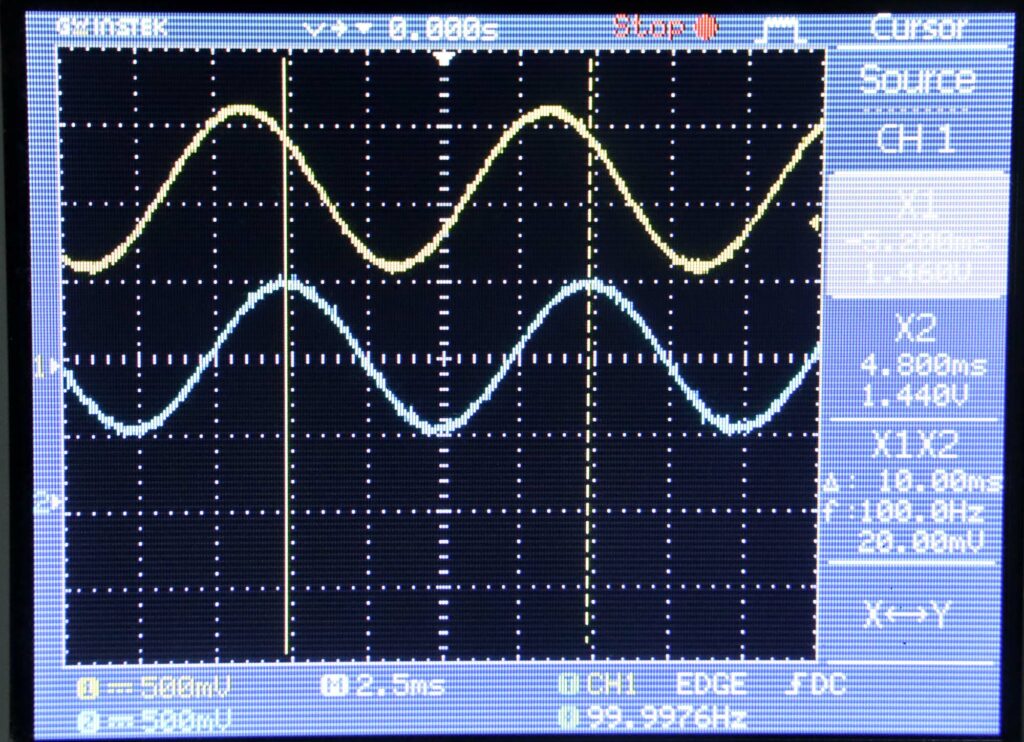
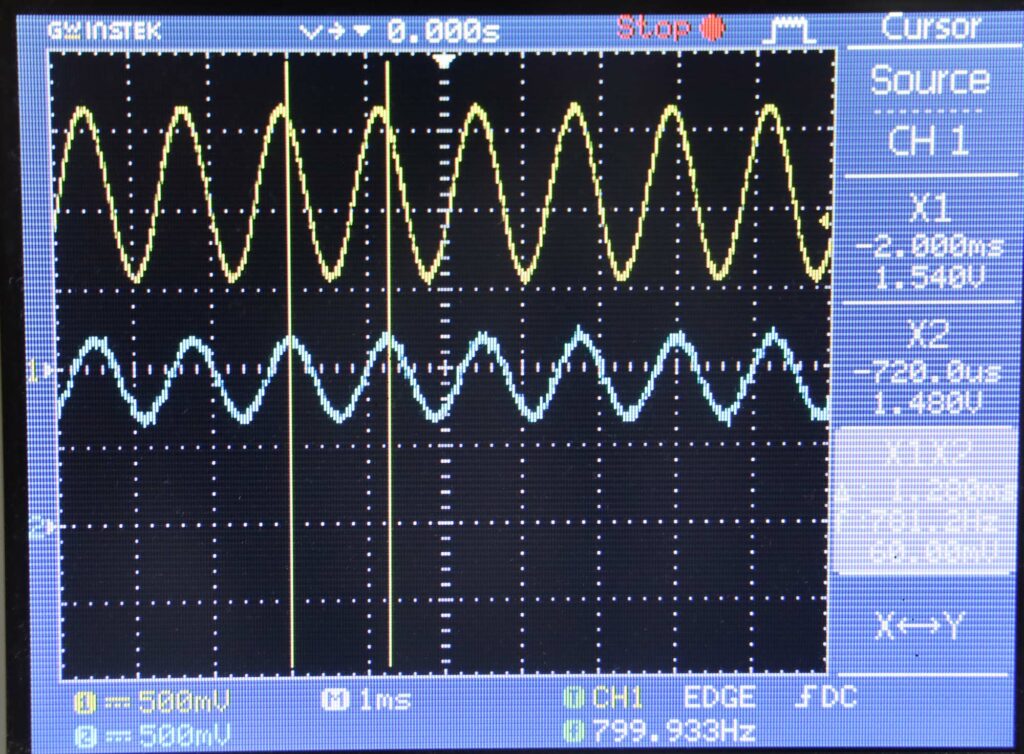
Berikut ini pengukuran pada frekuensi cut off = 100 Hz jauh di bawah frekuensi cut off.
Berikut ini pengukuran pada frekuensi cut off = 800 Hz. Amplitudo sinyal output sekitar 50% sinyal input.
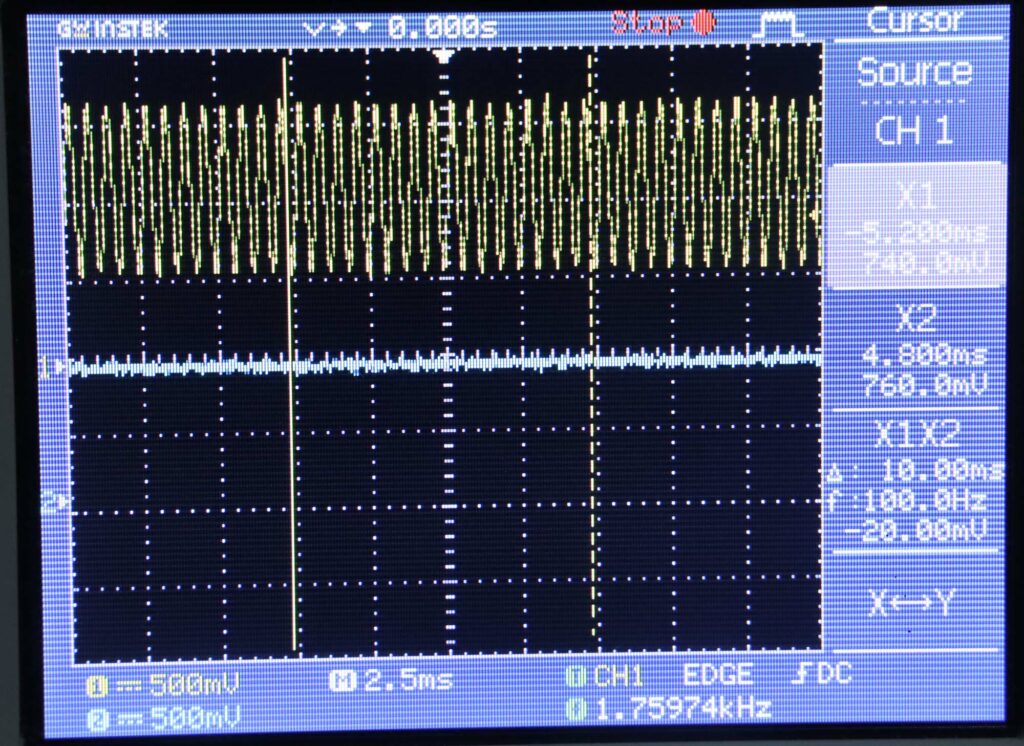
Berikut ini pengukuran pada frekuensi 1600 Hz, jauh di atas cut off. Amplitudo sinyal output kecil sekali hampir tidak ada.
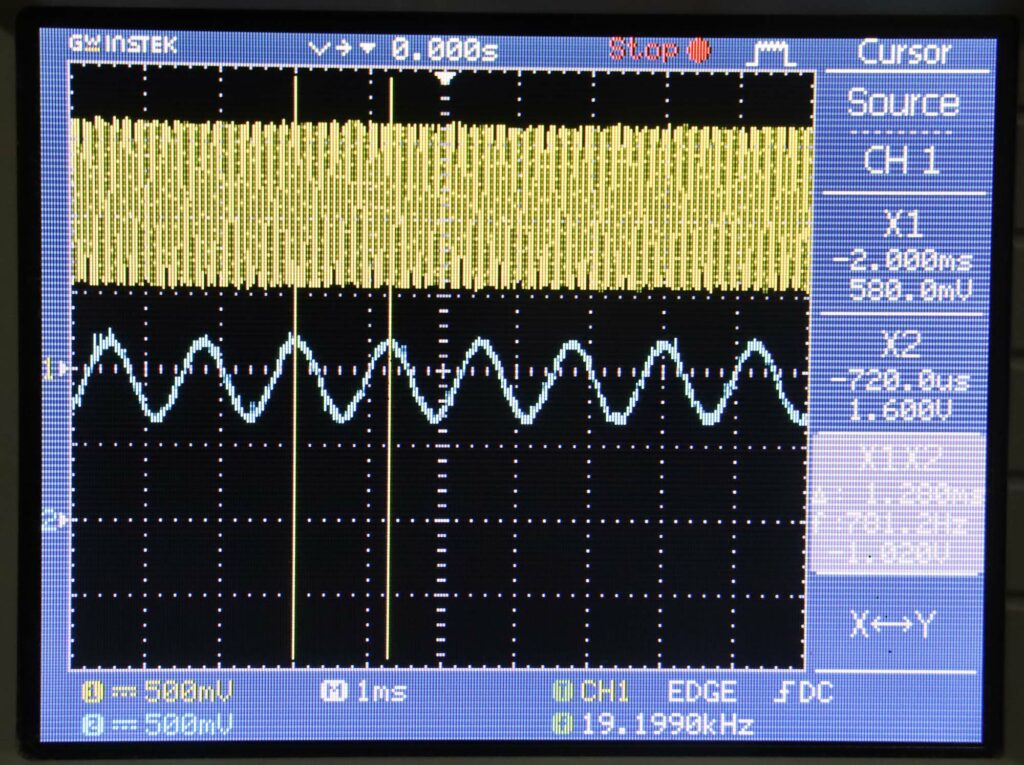
Berikut ini pengukuran pada frekuensi input 19200 Hz. Terjadi aliasing karena pada sistem ini tidak ada filter anti aliasing.